作业1 绘制金字塔（文件：Pyramid.java）

编写一个GraphicsProgram类的子类，绘制如下图所示的金字塔，该金字塔由砖块逐行堆砌而成，随着塔高递增，砖块的数量逐层递减 1。程序运行结果应当如下图所示：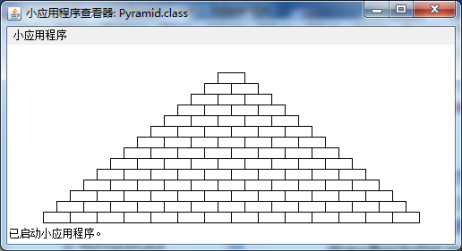

这个金字塔应该放置于窗口底部，居中对齐，并设置以下常量：
BRICK_WIDTH 砖块宽度 (30 像素 )
BRICK_HEIGHT 砖块高度 (12 像素 )
BRICKS_IN_BASE 底层砖块数量 (14)
括号里的数量对应上图的数值，在程序设计过程中，这个值应当是可以修改的。

作业2 绘制箭靶图形（文件: Target.java）

编写一个绘制箭靶图形的程序。程序运行结果应当如下图所示：

这3个圆形是对GOval类的三次简单运用（GOval类用于在图形窗口中显示椭圆），要求按正确的次序画出两红一白三个圆。最外侧的圆直径应为 100像素，白圆直径应为65像素，最里侧的红圆直径应为35像素。请在图形程序窗口中居中显示箭靶图形。

作业3 绘制GraphicsProgram类的子类（文件：ProgramHierarchy.java）

定义GraphicsProgram类的子类，用于绘制acm.program类的层次结构的一部分。程序运行结果应当如下图所示：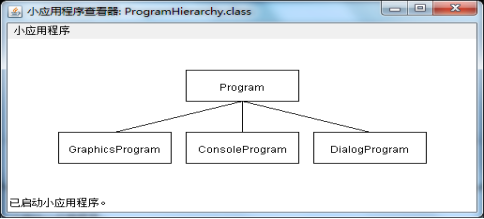

要绘制这个图形需要用到GRect、GLabel、和GLine这三个类。设计的重点是校准坐标值以确保矩形框图的各部分对齐。需要注意的是：
1.将框图的宽和高设置为命名常量，以便修改数值。
2.将标签置于所属矩形框的中心。通过调用label.getWidth() 和label.getAscent()能够获得标签的宽度和高出底边的数值。为使标签居中对齐，应当调整标签的起始位置使之位于矩形框各方向的中点位置。
3.连接两矩形框的线条，其两头应当分别接在对应边线的中点位置。
4.整体图形应当位于窗口的中心位置。

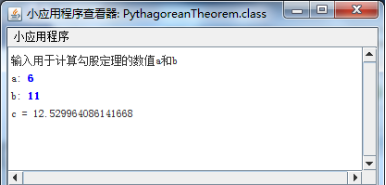
作业4 勾股定理计算（文件: PythagoreanTheorem.java）

高中几何课曾介绍过勾股定理 ( 即直角三角形三条边的长度之间的关系 ) ：
 c²=a²+b²
也可以写成以下形式：

这个表达式在Java中的书写形式在第六讲中已经介绍过，大家应该记得开平方的操作，这一操作可以通过调用数学类的标准方法Math.sqrt来完成。
例如，下列语句

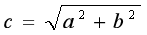
表示将 x  的平方根赋给 y 
请编写一个控制台程序，使之能通过用户给定的a,b的值，求出 c 的解，其中a,b为整型变量， c 为双精度浮点型。程序运行结果应当如下图所示：

作业5 找到最大值和最小值（文件: FindRange.java

编写一个控制台程序，使之能够读取一组整数，每行输入一个，直至读到 0 值时为止（在该程序中设0为循环结束标志，在编程实践中可以根据需要改变该值。）当完成对所有数据的读取后，该程序应当能够找出，并输出这一组数中的最大值和最小值。程序运行结果应当如下图所示：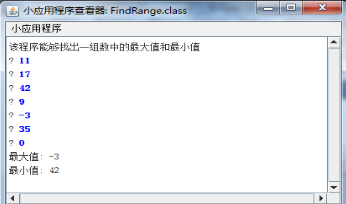

该程序应该能够对以下特殊情况进行处理：
1.如果在输入结束标志0前仅输入一个数值，则程序应当能够返回提示信息：”此数值既是最大值又是最小值。”
2.如果输入的第一个值就是循环结束标志0，则程序应当能够输出相应的提示信息："请输入一组整数！"

作业6 奇偶归一实现（文件: HailStone.java）

道格拉斯·侯世达的巨作《哥德尔、艾舍尔、巴赫——集异璧之大成》曾获得普利策奖，这本书中包含了许多数学谜团。这些谜团中的有不少可以借助计算机程序的形式表达。侯世达提出了一个重要的问题，而这个问题刚好在第6讲控制语句的研究范围中。
对于这个问题的描述，如下所示：
设存在正整数 n 。
若 n 为偶数，令 n=n/2 。
若 n 为奇数，令 n=3n+1 。
重复如上步骤，直到 n=1 为止。
侯世达用下述实例说明了这个过程，初值为 15 ：
15 是奇数，因此执行 3n+1 ： 46
46 是偶数，因此执行减半： 23
23 是奇数，因此执行 3n+1 ： 70
70 是偶数，因此执行减半： 35
35 是奇数，因此执行 3n+1 ： 106
106 是偶数，因此执行减半： 535
53 是奇数，因此执行 3n+1 ： 160
160 是偶数，因此执行减半： 80
80 是偶数，因此执行减半： 40
40 是偶数，因此执行减半： 20
20 是偶数，因此执行减半： 10
10 是偶数，因此执行减半： 5
5 是奇数，因此执行 3n+1 ： 16
16 是偶数，因此执行减半： 8
8 是偶数，因此执行减半： 4
4 是偶数，因此执行减半： 2
2 是偶数，因此执行减半： 1
从这个例子容易看出，数字在上下波动中，实际上到目前为止所试验过的所有整数，最终都会变小直到变为 1 为止。从某种角度而言，这个运算过程与冰雹（ hailstones ）有相似之处，后者在落地之前会反复被风吹向空中。也正因此，虽然有其它的名字，这个数列大多数情况下被称为冰雹数列（ Hailstone sequence ）。
写一个控制台程序，用户每输入一个数字，就用侯世达的书中相同的格式显示出该数字相应的冰雹数列，并在最后一行输出到达 1 所用的总步骤数。最终程序应当能显示如下结果：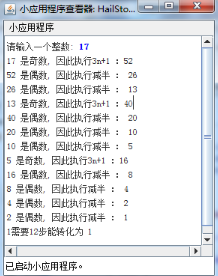

这个问题的迷人之处在于至今没有人能够证明整个过程最后一定会停下来。随着数值的变化，到达 1 所需要的步骤将能够变得非常大。不妨求解一下。当 n 等于 27 的时候，n需要多少步能转化为 1 ？